In this article we are going to have a look at a special kind of privacy-preserving cryptographic scheme: ORAMs. The acronym ORAM stands for Oblivious Random Access Machine, a technique used to anonymize the access flow between a trusted domain and untrusted data storage. As we will see, this has plenty of useful applications, with potentially practical impact for privacy and security. The idea, in a nutshell, is to not only encrypt the data at rest, but also dynamically shuffling it, so to make read and write operations indistinguishable to a malicious observer. Before we delve into the details, let us better explain the security scenario.
The Problem
In the modern digital world there is a substantial divide between local and remote resources: data which needs to be used at a certain location is often stored at rest at a different location, and only accessed when needed. This is done for reasons of cost, availability, and efficiency, both at a large scale (think of cloud storage) and at a small to very small scale (as in the case of a memory bus connecting the CPU to a memory bank.) Nowadays, even certain operating systems are often little more than an interface with a remote cloud provider. If on one side this has plenty of practical advantages, on the other side it raises issues of security and privacy.
Consider the example of a user operating on sensitive data stored on a remote server. How trusted is this server to the user? In an ideal world, the server’s role would only be that of serving the data to the user and recording the related modifications, but in practice many things can go wrong. The user can establish an encrypted connection to the server in order to secure the data from malicious third-parties sitting in between, but the server will eventually be the last bastion to the data keeping. The server’s own security might be lax, or the server itself could be malicious, intercepting or even modifying the user’s data.
One solution could be to enforce trust in the server itself, but this is not always possible or reasonable. Furthermore, in modern cloud infrastructures there is no single “remote server”, it is often very hard even to trace the position of a certain data chunk. This means that an effective solution should be trustless, only relying on the action of the user to secure the data.
An idea in this direction would be the one of encrypting the data stored remotely with a symmetric key locally kept by the user’s client application. Whenever the client needs to read data stored at a particular location, the client will request that particular encrypted data chunk to the server, the server will transmit it to the client, which will then decrypt it and read the decrypted data. If the operation involves writing data at a certain location, instead, the client will locally encrypt the data (with the same key), and will request to upload it to the server at the desired position. However there are two problems with this approach:
- the server will still be able to know which data location is being accessed; and
- it is pretty obvious whether the client is performing a “read” or “write” operation.
Both issues can be critical in practice. For example, a physician accessing a database of possible diagnostic test datasheets on behalf of a patient might expose the patient’s sensitive health conditions, financial information can be inferred by monitoring a stock exchange’s encrypted ledger, and so on.
Consider another example: a (trusted) CPU which needs to access data stored on an (untrusted) memory bank. In hardware design it is not uncommon to find situations where the CPU can be reasonably secured against external manipulation (for example as in smart cards), but doing so with the memory itself would prove to be impractical or very expensive. This is the reason, for example, why smart cards have usually only a few KiB of protected memory. While this is enough to store, e.g., encryption keys used to protect the rest of the bulk, untrusted memory, an adversary intercepting the communication bus between CPU and memory can still extract useful information and compromise the security of the system.
The above examples boil down to a simple point: encrypting data is not enough when the storage is not trusted, even if the storage is not malicious in the sense of mounting an active attack against the user, because access patterns can leak information. Informally speaking, an “access pattern” is the information that can be extracted by only looking at the communication channel and the state change of the storage before and after the operation. In practice, this is equivalent to considering the case of an adversarial storage system (server, memory bank, etc). More formally, the security model addressed by ORAMs is that of an “honest but curious” adversary: This adversary does not modify the flow of information (does not interfere with the protocol), but passively observes the access patterns of the user to extract secrets.
So, given that access patterns expose sensitive information, and that encryption alone is not enough to hide these access patterns, is there a working defense?
ORAM: The Idea
Formally speaking, an Oblivious Random Access Machine (ORAM) is a compiler, that turns any program into another program that has the same functionality of the original one, but such that the access patterns of the transformed program are independent from those of the original program. In order to achieve this, it is sufficient to replace read and write operations of the original program with oblivious read and oblivious write operations. An ORAM can hence be seen as a simulator that is seen as a memory interface by the CPU, and vice versa.
This definition is better understood in a client-server scenario (but the case of CPU-memory is analogous.) Consider the following, trivial example: A client C wants to perform read and write operations on a large database residing on a remote, untrusted server S. The database is encrypted with a symmetric key owned by C. Whenever C wants to perform an operation on the database, it does the following:
- C sends a request to S to download the whole database.
- C decrypts the whole database, performs the operation on the desired element, then re-encrypts the database (with the same key).
- Finally, C re-uploads the re-encrypted whole database to S.
Notice two problems here:
- If the operation is “write” (i.e. one or more elements of the database are modified) then S might detect the modification at a given position, because the encryption key is the same and hence might leave the encryption of untouched elements unaltered. This is fixable: in order to avoid this, C must use a randomized (i.e. semantically secure) symmetric-key encryption scheme, such as a block cipher with suitable mode of operation, variable IV, and a good source of randomness (so, no OTP or similar).
- This trivial scheme is clearly not efficient, because every time C must download and process locally the whole database. In the model we are considering, C might not even have enough storage to do this. So, another approach is necessary.
The idea of an ORAM is to achieve the same level of security of the above scheme in a more efficient way. Intuitively, it is necessary not only to re-encrypt part of the database with a randomized encryption scheme at every access, but also to shuffle the position of the re-encrypted elements. At a first glance, the workflow of an ORAM scheme is as follows:
- Given an element location/index on the database and an operation to perform on it, decide a subset of the remote storage that certainly (or at least with high probability) contains the desired element.
- Download from S that subset. This is more than downloading a single element, but less than downloading the whole database.
- Decrypt locally the subset downloaded.
- Find the desired element and perform the desired operation on it.
- Shuffle the position of some or all the database elements in the subset. C keeps track of the positions using an internal state.
- Re-encrypt the subset with a randomized scheme, using the same symmetric key stored by C.
- Re-upload the freshly re-encrypted subset to S.
There is clearly a tradeoff between performance and security, depending on the size of the subset, but with clever engineering the results can be optimized. Let’s see an example.
PathORAM
A huge advancement toward the realization of efficient ORAMs was achieved in 2012 with the scheme PathORAM, by Stefanov et al.
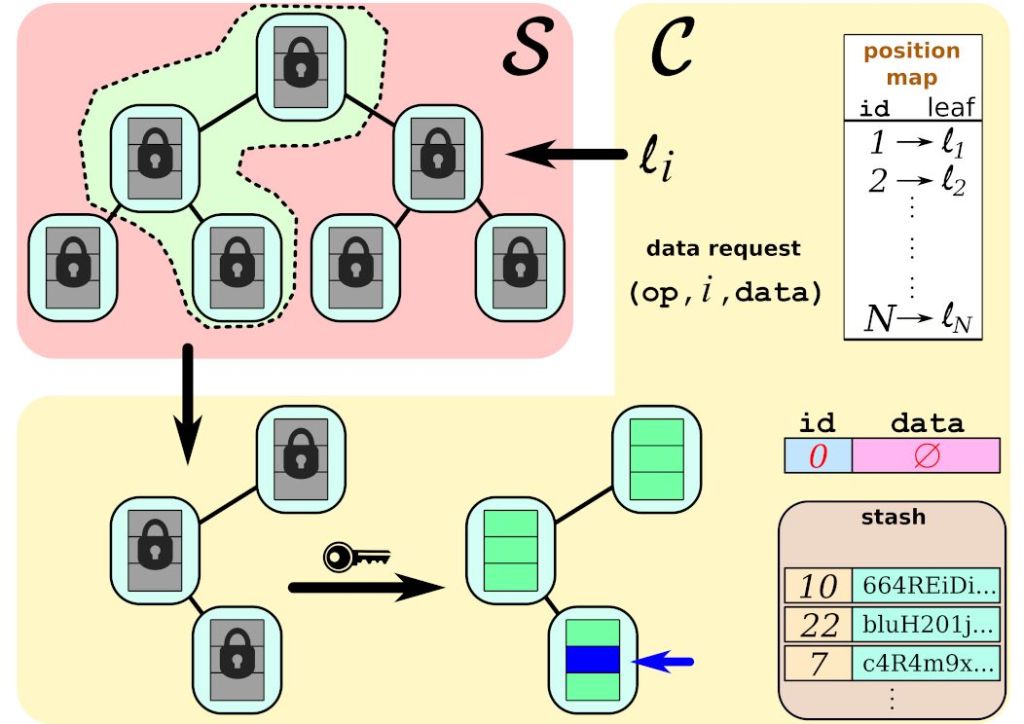
In PathORAM, a large database is stored on the server S arranged in a binary tree structure. Each node of the tree is a bucket that contains a fixed number (say, three in this example) of encrypted database blocks. Every block is encrypted through a semantically secure symmetric-key encryption scheme using a key that is stored on the client C.

From C’s point of view, a data request is a tuple (op, id, data), where op can be “read” or “write”, id is a database location identifier, and data is the new data to be written in the case of a write operation, or nothing in the case of a read operation. The client also stores locally a position map, which is a table mapping every database location id to a tree leaf identifier. As a first approximation, this locally stored table has so many entries as the number of elements in the database, so it might appear unclear what the performance gain is in respect to client storage. However notice that, in practice, a database block can be much larger than a single entry in the position map; moreover, we will discuss later how to further reduce the size of this table. Initially, during PathORAM initialization, the position map is initialized with random values.

When a data request is executed, C looks into the position map for the leaf identifier corresponding to the block identifier, and communicates this leaf identifier to S.

Notice how this leaf identifier uniquely pinpoints to a leaf in the binary tree, and hence to a single, complete branch between the root of the tree and the leaf.

This branch (which size is only logarithmic in the size of the database, hence the communication gain) is then sent by S to C, where every block contained within is decrypted. All decrypted blocks are then sequentially inspected by C. A decrypted database block consists of a position identifier and a data chunk. There cannot be two identical position identifiers in the whole decrypted database, except for a specially chosen one (let’s say 0) which denotes an “empty” or “unassigned” block.

The idea of the shuffling in PathORAM is as follows:
- The position map is done in such a way that we are guaranteed that the block with the desired id is among those in the branch transmitted by S.
- If an empty block is found, it is (initially) left untouched.
- Any non-empty block is swapped with the empty block farthest away from the root in the current branch, but such that its leaf path has a common intersection with the current branch.
- The process is repeated for every block in the branch. When the desired block from the data request is found, though, its identifier in the position map is assigned a new random value.
- If no empty blocks are found, the block being shuffled is temporarily stored locally in an “overflow stash” by C instead, and replaced with a new empty block. It can be proven that the size of this stash grows very slowly on average, so it can be efficiently stored by C.
- When all the blocks have been processed this way, try to reassign blocks temporarily stored in the stash to newly created empty blocks in the branch, so to flush the stash.
- Finally, the whole branch is re-encrypted and re-uploaded to S.
Let’s see concretely how it works. C starts scanning the decrypted branch from the root. Let’s assume that the first block has a 0 identifier. This means that it is an empty block, so C does nothing and keeps scanning.

The second block is non-empty, so it must be shuffled.

C looks at the position map to identify the related leaf

There is a node (bucket) at the intersection between the current branch and the newly identified branch. This bucket is currently decrypted by C, so it is now scanned to look for a new empty block.

The first block is not empty.

The second block is also not empty.

C finds an empty block at the third attempt.

C swaps the two blocks. Notice how the empty block is pushed closer to the tree root.

Then C resumes the scan of the path toward the leaf of the branch, and keeps performing shuffles for every non-empty block that has not already been shuffled before.

At some point, eventually C will find the desired block from the data request. First of all, C will perform the data request (read or write).

Then, C will update the position map for that block with a newly generated random leaf identifier.

This new random value will identify a new branch in the binary tree, which will partially intersect the current branch. C will start looking at the lowest intersection node (farthest away from the root) for an empty spot to swap the current data block.

When an empty block is found, the two are swapped as before.
However, for any of these swaps, it might happen that no empty block is found in the considered node. If this is the case, C goes up one node toward the tree and keeps looking for an empty block to perform the swap.

In any case, after a swap is executed C keeps scanning the branch until the end.

However, it might happen that for a certain block, no empty spot is found at all, regardless of how closer to the root C goes. This means that the current branch is completely filled above the element, and there is no room for other swaps. The solution, in this case, is to temporarily “park” exceeding blocks in an additional local store, called stash.

At the same time, the currently scanned block is overwritten with an empty one, thereby freeing one slot in the branch.
Periodically, the content of the stash is moved back into empty slots along the branch with a suitable leaf index if available. Finally, the branch is re-encrypted with the encryption key and re-uploaded to S.

From S’s point of view, all it can be seen is the access pattern, that is the communication channel between A and C and the change of state in the encrypted tree.

Further Considerations
The above is just a very simplified view of PathORAM. Many improvements in security and performance are possible.
First of all, as already noticed, the size of the position map is linear in the number of elements of the database. This can be good enough for some applications, but it can be improved by using recursion: The idea is to store the position map for a certain ORAM inside another, smaller ORAM, and only keep in C the smaller position table for the new ORAM. The process can be repeated, yielding a tradeoff between the storage required on C for the position map and the communication complexity between C and S.
Another good practice is to use an authenticated encryption scheme (AE) instead of a simple randomized encryption scheme. This would prevent attacks that go beyond the notion of honest-but-curious adversaries, but that can be anyway problematic in a networked scenario because of the possibility of modifying encrypted blocks.
It is also important to notice that there is other ways to construct ORAMs, not always based on binary trees. Some further improvements involve the use of multiparty computation and homomorphic encryption to achieve speedups or extra features.
ORAMs have the advantage of being simple and relatively efficient, but there are other cryptographic primitives that can achieve similar tasks. Conceptually similar to ORAM is Private Information Retrieval (PIR), that has the advantage of being suited to a multi-user environment, but offer different security guarantees and has the disadvantage that the server is required to perform a certain deal of computation (unlike ORAMs where all the computation is local).



4 comments