SPHINCS is the state-of-the-art algorithm in the category of stateless hash-based signatures. It’s quantum-safe, and thus a potential contender in NIST’s post-quantum crypto standardization project. SPHINCS is the culmination of decades of research on hash-based signatures, and since its publication in 2015 hasn’t been subject to any attack, nor any improvement.
In the first post in this series we explained how SPHINCS can be improved thanks to the following trick: instead of generating a list of random numbers using a hash function (where you may have duplicates), generate a list of distinct random numbers using a pseudorandom generator. Our paper Clarifying the subset resilience problem analyzes in detail the security benefits of such a construction.
This new post summarizes the contributions from a second paper we published recently, Improving Stateless Hash Functions, also based on research made during Guillaume‘s masters thesis at Kudelski Security (his full report is available).
Again we’ll describe in a non-technical way the optimizations proposed to SPHINCS: secret key caching, batch signing, mask-less hashing, and last but not least Octopus authentication. But first, we’ll try to give a glimpse of how SPHINCS work, without the technical details.
(The optimizations described in this post are the basis for Gravity-SPHINCS, a variant of SPHINCS that we’ll submit to NIST’s project. By the way, we’ve created the page https://post-quantum.ch to track submissions announced as candidates.)

The 4 trees in SPHINCS
The SPHINCS signature scheme is not of the simplest kind, and is hard to understand by only reading its informal specification. So instead of trying to explain it fully, we’ll just describe its general structure, which can be seen as the combination of four types of trees:
- The main hyper tree, of height denoted
(60 in SPHINCS-256). The root of this tree is part of the public key. The leaves of this tree are HORST instances (type-4 trees). This hyper-tree is divided into
(12 in SPHINCS-256) layers of type-2 trees.
- The subtrees, which are Merkle trees of height
(
in SPHINCS-256). The leaves of these trees are roots of type-3 trees; said roots are compressed public keys of WOTS instances, that connect to a tree at the next layer.
- The WOTS public key compression trees, which are L-trees (and not necessarily complete binary trees), of height
when there are
leaves. The leaves of this tree are components of a WOTS public key (67 values of 256 bits each in SPHINCS-256). The associated WOTS instance signs a tree root at the next layer.
- The HORST public key compression trees, at the bottom of the hyper-tree, are Merkle trees of height
, where
is the number of public key elements in the HORST instances (
in SPHINCS-256).
You already know HORST, but maybe not WOTS, which stands for Winternitz One-Time Signature: in the hyper-tree of SPHINCS, WOTS instances are used to sign children node. See for example David’s post for a simple introduction to WOTS.
The hyper-tree structure can be visualized as in the figure below:

Signing with SPHINCS then works like this:
- Derive a leaf index from the message and the private key. This index identifies one of the
HORST instances (relative to the hyper tree), that will be used to sign the message.
- Generate the HORST instance whose seed is derived from the private key and from the leaf index, and sign the message with this HORST instance. The HORST signature includes several keys and their respective authentication paths, and is part of the SPHINCS signature. Obtain the HORST tree-compressed public key $p$.
- For each layer of the hyper-tree, sign the public key
(obtained from the lower layer) using the correct WOTS instance (derived from the leaf index); add this WOTS signature and associated type-3 authentication path to the SPHINCS signature. Compute the authentication path of this WOTS instance within the type-2 subtree; add this path to the SPHINCS signature and let $p$ be the subtree root.
And that’s it. This is really a bird eye’s view of SPHINCS, and we omitted many details, but hopefully this will help you understand the optimizations described below.
Secret key caching
Every time a SPHINCS signature is computed, the tree in the root layer of the hyper tree has to be recomputed. This reduces the key size by just storing the root, but adds additional computations and increases the signature size. A possible trade-off is therefore to view this top Merkle tree as part of the secret key, as depicted in the figure below:
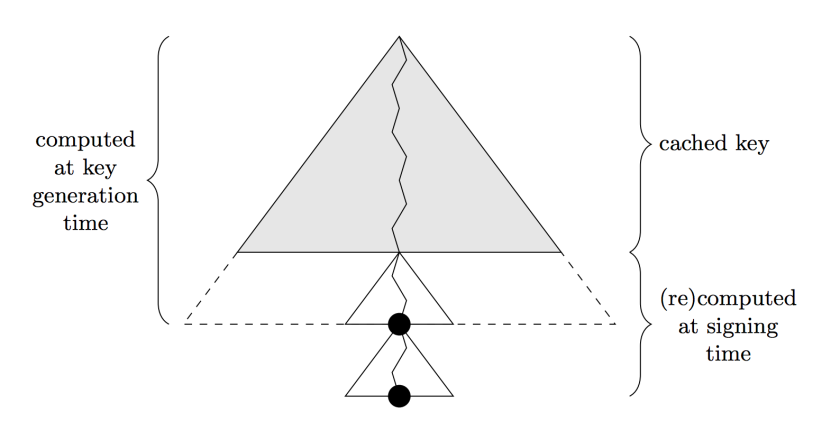
Using this trick, we can use a top tree of 20 layers and cache 15 of these, which is equivalent to about 2MB of data. This reduces the signature size of 201 hash values, or 6432 bytes, and speeds up signature generation and verification because fewer WOTS instances have to be computed.
Batch signing
In simple terms, batch signing is a technique to sign multiple messages at once, much faster than if all messages were signed independently. The core idea is simple: instead of signing an actual message, sign the root of a Merkle tree whose leaves are the messages—yet another tree! You can visualize this as follows:

To verify the signature of a single message, you would just provide the authentication path of the message. Applied to SPHINCS, batch signing can be exploited to reduce the size of the underlying trees, since fewer signatures would be needed for a same number of messages (remember that SPHINCS needs such a huge tree in order to support the issuance of a large number of signatures).
For example, with 1024 messages per batch and keeping the bound of messages per key pair, SPHINCS can be tweaked to save 4286 bytes per signature.
Mask-less hashing
In the original SPHINCS, values to be hashed within a Merkle tree are first XORed with pseudorandomly generated values called masks, as shown below:

Using such masks has pros and cons:
- Pros: it guarantees that the scheme is secure even if the hash function is not collision resistant (but only second-preimage resistant)
- Cons: it complicates the construction, and increases the key size to about 1KB
We believe that having collision resistant hash functions is a totally reasonable assumption. Actually, you’ll always need a collision-resistant function to hash the message in the first place.
Octopus authentication
What we call Octopus is a simple, yet powerful idea. First, recall the notion of authentication path from a previous article, and observe that a SPHINCS signature includes authentication paths for several hashes within an HORST tree. Nothing’s wrong here, but there’s room for optimization because the list of such paths may include redundancies. Specifically, several authentication paths may overlap, and therefore include the very same nodes; the SPHINCS signature will then include several copies of the same hash value. How to get rid of these?
In Octopus-speak, we call authentication paths tentacles. When two tentacles merge—that is, when paths reach the same node when starting from the bottom of the tree—then octopus provides an algorithm to only keep a unique copy of each node, and totally eliminate redundancies. The figure belows shows a simple example of tentacles merging, where black nodes are the ones to authenticates, dark grey nodes are in the authentication path, and light grey nodes are computed:

The idea of octopus looks straightforward, but the analysis is not, see pages 10-14 in our paper. The upshot is that this trick leads to SPHINCS signatures shorter of 1909 bytes on average (the actual signature size varies depending on the message, because different messages will lead to different sets of tentacles).



One comment