Introducing ABE Squared: A Framework for Comparing the Efficiency of ABE Schemes

Authors: Antonio de la Piedra (Kudelski Security Research Team), Marloes Venema (Radboud University Nijmegen), Greg Alpar (Radboud University Nijmegen and Open University of the Netherlands).

Attribute-based encryption (ABE) is an elegant type of public-key cryptography where secret keys are associated to attributes. It can be used for fine-grained access control on sensitive data, and the Cloud is a perfect use case.

In the past, we have shown how Attributed-based encryption schemes can be attacked. This time, we asked ourselves the following question: Given the myriad of published ABE schemes, can we accurately measure their efficiency in order to know which one is the best? And if yes, what is the best way of achieving this, and what do we mean by the best?

In order to answer this question, we have created ABE Squared, a framework for comparing the efficiency of ABE schemes and to optimize them according to the design goal, taking into account different optimization layers.

We are presenting ABE Squared this week at CHES 2022.

Attribute-based Encryption

An ABE scheme generally consists of 4 algorithms: Setup, Key generation, Encryption and Decryption. In a typical ABE deployment, a party, e.g. Alice, wants to protect her sensitive data according to a particular access policy based on attributes e.g. doctor OR nurse. In order to do that, Alice will request to a Key Generation Authority (KGA) the master public key (MPK) of the system, and she will encrypt her data accordingly.

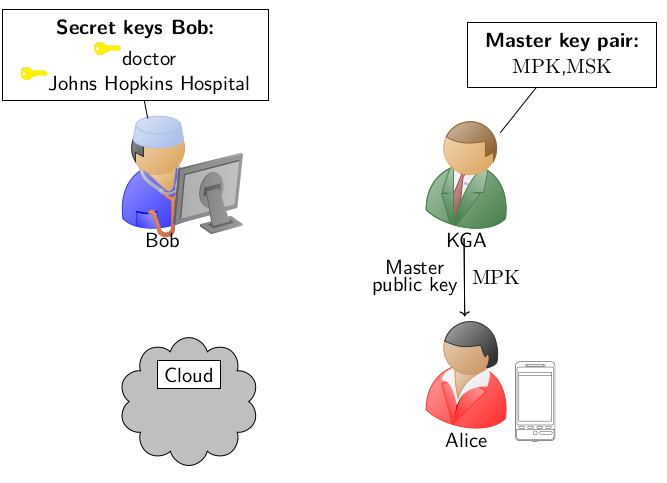
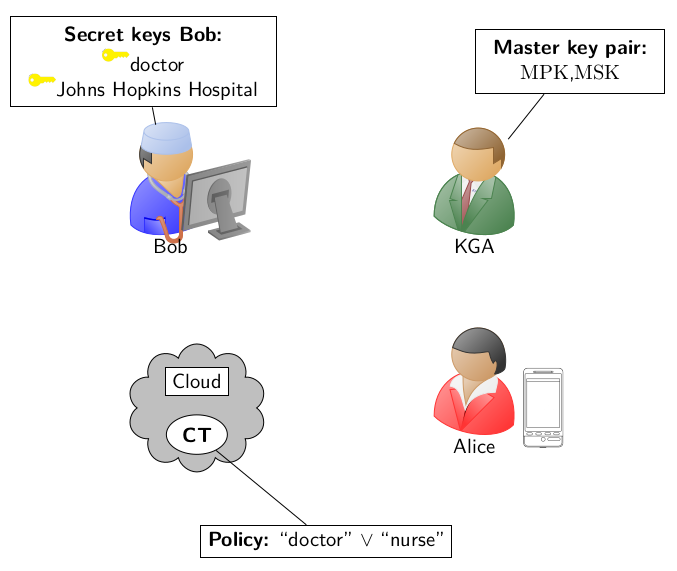
Only parties having secret keys related to the attributes doctor, nurse can satisfy the access policy established by Alice and decrypt. In our example, Bob receives to secret keys related to the attributes doctor and Johns Hopkins Hospital, which satisfy (in this case, doctor) the access policy established by Alice.

Nowadays, mature ABE schemes mainly rely on pairing-based cryptography and are challenging to implement. Many of these implementations of ABE schemes rely on rapid prototyping frameworks such as CHARM and oftentimes only some parts of the scheme are optimized. This can be problematic, since implementing an ABE scheme requires addressing many variables such as the implementation of access policy, the group arithmetic and the type conversion. All these areas depend on the type ABE application we are designing. To aid the design process of an ABE application, improve the benchmarking capabilities of designers of ABE schemes and to provide heuristics capable of obtaining optimized versions of ABE schemes given design goal, we have created ABE Squared.

ABE Squared

ABE Squared takes into account all the layers of optimization. As inputs, it receives the theoretical description of the scheme and produces the description of the scheme that directly yields the most efficient implementation.

In this process, we choose the design goal, which is of utmost importance. For instance, some applications may require an optimized key generation variant, such as the implementation of a KGA. In order to achieve this, every layer needs to be optimized, and we create optimization approaches based on these design goals:

1. We first analyze the arithmetic and group operations used in the schemes by benchmarking their efficiency in the paring-friendly groups that can be used.
2. We show how the order of computations can be optimized, given the efficiency of the available algorithms for arithmetic in the chosen pairing-friendly group.
3. We show how the schemes can be instantiated in these group so to obtain the best possible efficiency, given a particular design goal. To this end, we provide new manual and heuristic techniques to convert the scheme from type 1 to type 3 and obtain the following variants of the scheme: optimized encryption (OE), optimized key generation (OK), optimized decryption (OD) and balanced approaches such as key generation/encryption and encryption/decryption.

The design goal matters

In order to show how important is to have a design goal when implementing an ABE scheme, we have taken the Wat11-I scheme and implemented using the BLS-12-381 pairing-friendly curve.

We have used all of our heuristics to obtain the OD, OE and OK variants of the same scheme:

• If we compare an optimized key generation variant with a variant that has been optimized to encryption or decryption, we see that the latter requires 143 % more cycles that the former.
• If we compare an optimized encryption variant with a variant that has been optimized for key generation, we see that the latter requires 153.3 % more cycles than the former.
• Finally, if we compare an optimized decryption variant with an implementation optimized for key generation we see that the latter requires around 8 % more cycles. In this case, the percentage is small, because in ABE, the decryption algorithm involves mainly pairings operations and less group operations.

Comparing ABE schemes using ABE Squared

Another question we can ask is: What scheme is the best for which operation (e.g. key generation, encryption, decryption) and using which pairing-friendly curve? To illustrate how ABE Squared works, we have chosen 3 ABE schemes that share the same practical properties and structure: AC17-LU, Wat11-IV and RW13.

We see that, in general, the BLS-12-381 pairing-friendly curve provides the best performance. Moreover, the AC17-LU is the best scheme for performing encryption and decryption, whereas the RW13 scheme is the best scheme for key generation.

We started this article by asking ourselves what could be the best way of measuring the efficiency of ABE schemes. We have seen that only by first optimizing the schemes to the same design goal we can compare them in a fair manner. If you want to know more about our optimization heuristics and ABE Squared in general, you can read our paper in the IACR ePrint service.