When Constant-Time Source Code May Not Save You

On November 14 at CANS 2016 in Milan I presented a timing attack against an implementation of Curve25519 (also called X25519).

This elliptic curve was designed by DJ Bernstein in order to provide a secure curve without probable NSA back doors and with safe computations. Additionally it was designed to be protected against state-of-the-art timing attacks.

The targeted implementation called Curve25519-donna essentially follows the prescriptions of the informational RFC 7748 Elliptic Curves for Security. The purpose of this recommendation is to avoid the use of weak ECC designs containing timing-dependent instructions.

While it is a good idea to set some minimum security requirements, those are generally not sufficient. I will show this with a timing attack against Curve25519-donna.

The implementation is publicly available on Github and follows Bernstein’s first design. It is used for the computation of a shared secret with ECDH.

This blog post will not provide all the details of the attack. If you are interested in knowing more, have a look at the paper When Constant-Time Source Yields Variable-Time Binary: Exploiting Curve25519-donna Built with MSVC 2015.

Presentation of the implementation of the curve

The equation of the elliptic curve is given by over the field with .

The computations are only executed on the X-coordinate. The value of a coordinate can be seen as a large integer and this integer can be written as a polynomial in order to improve the computations: with . The value of the integer is given by . This allows storage of 10 coefficients with a bounded value.

There is no point validation: any 32-byte integer can be given as a point and the multiplication will be executed safely. There are however two restrictions on the private key: the leading 1 must be at bit position 2 and the last three bits must be zero.

For scalar multiplication Curve25519-donna uses a specific implementation of the Montgomery ladder allowing the execution of the exact same instructions whether the key bit value is 0 or 1.

Setup

The idea of the timing attack is to measure the time needed for a user to compute the shared secret with the point we sent them. If the timing needed depends on the input, the next step consists of finding a link between the timing leakage and some secret data, for example a secret key.

In our case we want to recover the secret key used to compute the shared secret in the ECDH protocol. For this we only have access to the time required to do the computation of the multiplication of a point and the secret key, as shown in Figure 1.

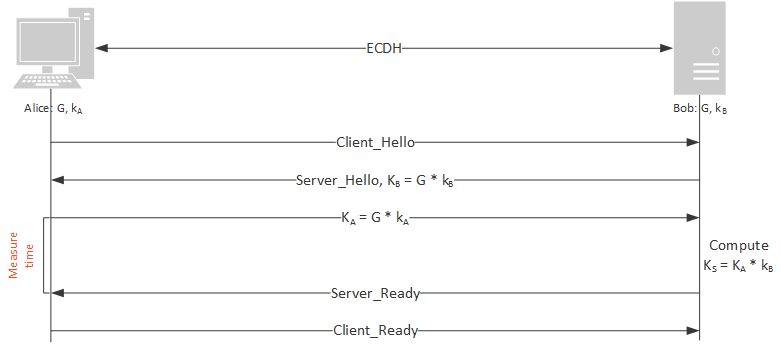
In order to measure the timings, the Intel assembly instruction rdtsc (read time stamp counter) was used. To make the measurements more stable, it was called the following way:

getTicksBeginning();
getTicksEnd();
getTicksBeginning();
getTicksEnd();

start = getTicksBeginning();
// Code to be measured
end = getTicksEnd();

With:

unsigned long getTicksBeginning() 
{
    unsigned long time;
    __asm {
        cpuid         // Force in order execution
        rdtsc         // eax = counter time
        mov time, eax // time = eax
    };
    return time;
}
unsigned long getTicksEnd() 
{
    unsigned long time;
    __asm {
        rdtscp        // eax = counter time
        mov time, eax // time = eax
        cpuid         // Force in order execution
}; return time; }

The computation was executed and timed locally on a Sandy Bridge 64-bit Windows 7 PC with Intel i5-2400 processor: 3.1 GHz, 4 cores, 4 threads. It should be noted that the code of the curve was compiled for 32-bit architectures using MSVC 2015.

Timing Leakage

A dependence of the computation time on the input value can be revealed by comparing the timings obtained by computing multiple times the scalar multiplication with the same key and the time taken to compute multiplications with different keys . The results are shown in Figure 2.

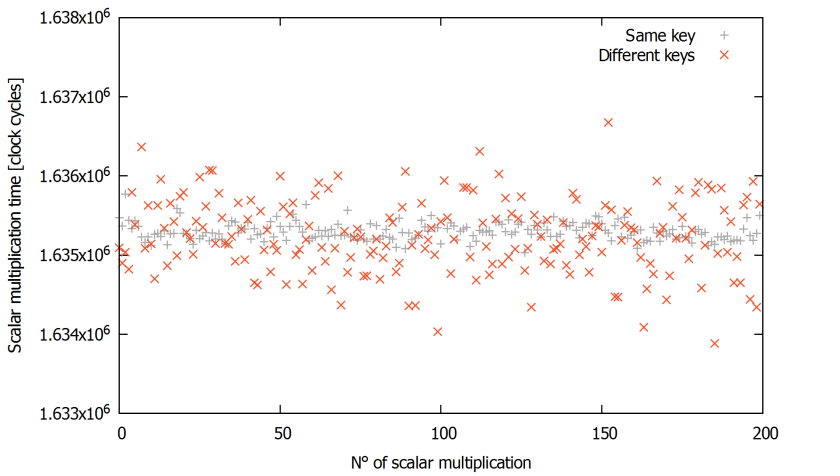
The computation times of the multiplication with the same key are shown in grey and the timings of the multiplications with different keys are shown in orange. We can see that the timing distribution of the orange crosses varies much more than that of the grey pluses.

The second part of the attack consists of finding the origin of the leakage and seeing whether it is exploitable.

Looking carefully at the assembly code we discover that the timing leakage is coming from a run-time library of Windows: llmul (see code below). These assembly instructions perform the multiplication of two 64-bit integers. Here the timing difference is introduced when the 32 most significant bits (MSB) of both operands of the multiplication are all zero. In this case the multiplication of the 32 MSB is omitted, as shown in orange in the following code:

 title llmul - long multiply routine
;***
;llmul.asm - long multiply routine
;
; Copyright (c) Microsoft Corporation. All rights reserved.
;
;Purpose:
; Defines long multiply routine
; Both signed and unsigned routines are the same, since multiply's
; work out the same in 2's complement
; creates the following routine:
; __allmul
;************************************************************************

.xlist
include vcruntime.inc
include mm.inc
.list
 CODESEG

_allmul PROC NEAR
.FPO (0, 4, 0, 0, 0, 0)

A EQU [esp + 4] ; stack address of a
B EQU [esp + 12] ; stack address of b

 mov eax,HIWORD(A)
 mov ecx,HIWORD(B)
 or ecx,eax ;test for both hiwords zero.
 mov ecx,LOWORD(B)
 jnz short hard ;both are zero, just mult ALO and BLO
 mov eax,LOWORD(A)
 mul ecx
 ret 16 ; callee restores the stack
hard:
 push ebx
.FPO (1, 4, 0, 0, 0, 0)
A2 EQU [esp + 8] ; stack address of a
B2 EQU [esp + 16] ; stack address of b
 mul ecx ;eax has AHI, ecx has BLO, so AHI * BLO
 mov ebx,eax ;save result
 mov eax,LOWORD(A2)
 mul dword ptr HIWORD(B2) ;ALO * BHI
 add ebx,eax ;ebx = ((ALO * BHI) + (AHI * BLO))
 mov eax,LOWORD(A2) ;ecx = BLO
 mul ecx ;so edx:eax = ALO*BLO
 add edx,ebx ;now edx has all the LO*HI stuff
 pop ebx
 ret 16 ; callee restores the stack

_allmul ENDP
 end

This function is called from the function fscalar_product which simply computes the multiplication of the coefficients with a constant integer. The type limb is a 64-bit integer.

static void fscalar_product(limb *output, const limb *in, const limb scalar) {
    unsigned i;
    for (i = 0; i < 10; ++i) {
        output[i] = in[i] * scalar;
    }
}

In the elliptic curve implementation the 32 MSB of the coefficients are only not zero when they are negative (two’s complement is used to represent the negative numbers). Thus we can say that it takes more time to process a negative coefficient than a positive coefficient.

To corroborate this finding, let’s compare the timing measurements for negative and positive coefficients:

It can be seen that on average the multiplications with negative coefficients take more time than those with positive coefficients.

The next step is to mount an attack taking advantage of this leakage.

We need to find a link between the key bit processing time (where the leakage appears) and the overall computation time that we can measure. To do so the idea is to see the overall computation time as the time to compute the processing of a key bit , plus the time to compute the processing of the key bits and the key bits , for a given base point P:

We can make the assumption that the time to process the other bits (than the targeted key bit ) is random (Gaussian). Then in average over  executions, we have:

And it follows that for two sets of base points A and B, :

If , then

With base points selected at random in the sets A and B, the average of the times required to process the key bit only tells us that in average the time to compute the processing of the key bit took more time with the base points in A than those in B. We have to select the base points in a way that allows the differentiation of the value of .
Let’s define two sets:
: set of base points causing more negative coefficients in the polynomial representing the coordinate of the point being added in the Montgomery ladder when
: set of base points causing more negative coefficients in the polynomial representing the coordinate of the point being added in the Montgomery ladder when

Then we have: and otherwise.

We have found a link between the leakage and the key bits values. The timing attack can be performed.

Timing Attack

As the timing measurements can vary significantly for the same execution depending on the processes handled by the processor, the measures have to be repeated many times.

The idea is to perform the attack bit per bit and construct a key sequentially with the bits found. For each bit of the key, the algorithm is the following:

1. Find 200 base points in and 200 in . To do so, we simply select base points (integers) at random and count the number of negative coefficients in the polynomial representing the coordinate of the point being added for the key bit we are interested in. For that we use the key constructed with the previous bits found and the computation is done locally.

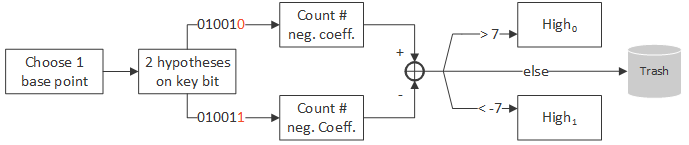
2. Measure the timings for every base point. To do so, each measurement is repeated 25,000 times (found empirically) and we take the 15 minimum values among them. Then we take the average value of these 15 timings.

3. Finally, we take the mean of the timings of the base points in and the mean of the base points in and we compare those two values.

These steps are repeated for the same key bit until we get twice the same value. So in the worst case the algorithm is repeated three times per bit of the key.

Results

The attack was successfully performed locally. An example of timings is shown in Figure 3.

It should be noted that the attack takes about 1 month to recover the entire key in our setup. 25,000 measurements take about 15 seconds, there are 400 base points and the measurements can be repeated up to three times. 251 key bits have to be recovered.

Once a bit is wrongly recovered the following bits cannot be trusted as we select the base points for another key.

In order to test the feasibility on the Internet, some communications delays were added to the measurements. The attack was still successful.

Several optimizations could be implemented. For example feedback on the key bits found, brute force once there are only few key bits to recover, parameters optimizations, etc. However the purpose of this work was not to exploit the weakness in this specific implementation.

Conclusion

Simply following the recommendations of the RFC and having a “constant-time” source code is not sufficient to prevent timing leakage. Once a security design is implemented, whatever effort is put into protecting each part of the code, there still remains a strong possibility of a timing leak. It is virtually impossible to have control over all the parameters at stake. Compiler and processor optimizations, processor specificity, hardware construction, and run-time libraries are all examples of elements that cannot be predicted when implementing at a high level.

The attack developed shows that the effects of these low-level actors can be exploited practically for the curve X25519: it is not only theoretically possible to find weaknesses, they can be found and exploited in a reasonable amount of time.

Nevertheless, the idea of ensuring that the design itself is secure by using a formalized approach such as RFC is an important step in minimizing the side-channel leakage of any final system.

This attack also highlighted a potential weakness induced by the Windows run-time library: every code compiled in 32-bit with MSVC on 64-bit architectures will call llmul every time a 64-bit multiplication is executed.