During the Hardwear.io 2022 conference, Nicolas and I presented hardware attacks against the SM4 block cipher. In this post, I’ll give more details about the fault attacks we presented and the tools we have released.
We started to study this algorithm when we found the CH569w SoC from WCH containing a hardware accelerator doing SM4. Then we figured out that SM4 is the de facto standard in China, and it seems to be more and more deployed. For example, ARM introduced two instructions since ARMv8.4, sm4e a sm4ekey to speed up SM4 computation. RISC-V also integrated two instructions doing similar accelerations.
According to the draft IETF, SM4 is a block cipher taking a 128-bit key and performing 32 rounds on a 128-bit plaintext block. Like AES, it is composed of a key schedule. It generates 36 round keys of 32 bits each. The first four round keys are the secret key XORed with the constants FKs called the family keys. Then, each round key is generated according to the following diagram, where the CKs are constants defined in the standard.

For the following, as a notation, all the uppercase letters describe 32-bit words and lowercase letters are bytes. During one round, only one new round key is generated, the other three are simply shifted on the right. Thus, from four consecutive round keys, the algorithm is invertible.
The last 32 round keys are used during the 32 rounds of the encryption or the decryption of a block. One round of SM4 is very similar to the key schedule. A round transformed a 128-bit state into another state with the following operations:
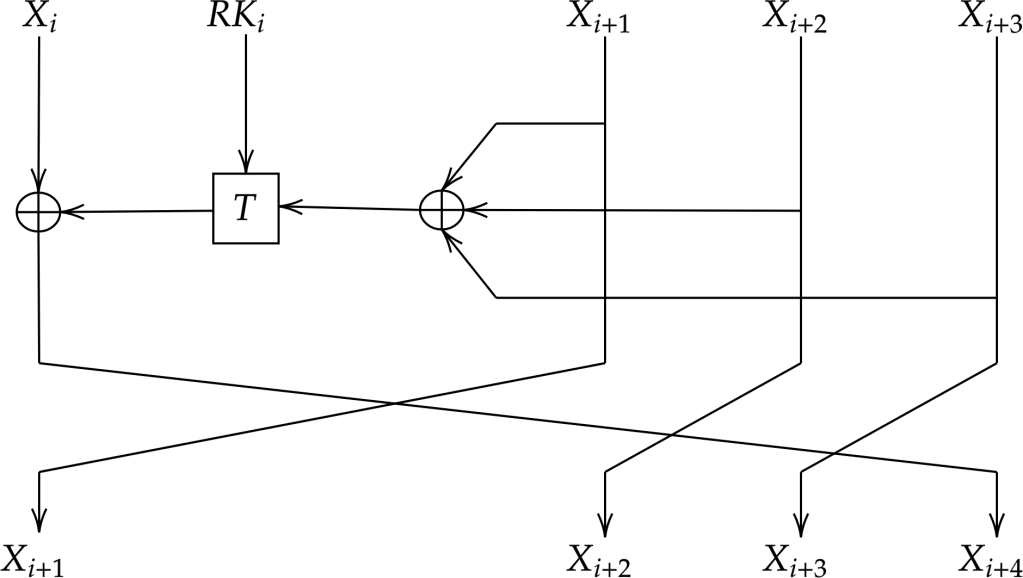
One of the differences with the key schedule is the T function which is slightly different than T’ of the key schedule. The function T works according to the following diagram:

Where L is a linear transformation with 32-bit input and 32-bit output. Used for diffusion among a word. S are S-Box with 8-bit input and 8-bit output. Similarly as for AES, the Sbox is based on inverse and affine transformations.
The first fault attack in the literature was published in 2006 by Zhang and Wu. The paper is written in Chinese, but the attack is a basic block for all further fault attacks, and some papers in English give a nice description of this attack. The idea of this fault attack is to introduce a random byte in the second, third, or fourth word at the input of the last round. Thus the fault is directly observable in the ciphertext since these words are simply shifted during a round. The T function input is also corrupted and its output is observable in the ciphertext. For example, a fault in the third word of the last round results in the following:
The idea of the attack is to recover a byte k of the last round key by applying differential analysis from the random byte fault 𝛼 introduced. It starts by writing the formulas of difference of the Sbox output:
All the Sbox inputs are replaced by the variable x for simplicity. Then the attack proceeds backwards until the output of T by applying the inverse of the L function:
We obtain a word with only one non-zero byte. It matches the position of the byte fault injected. Now the problem is to find an unknown byte x such that:
To solve this problem, the attack builds a static table IN such that
This table is unique for the SM4 SBox. It contains the set of x satisfying the previous equation. Building this table would give that for each entry, we would have on average only two different x. The attack proceeds as follow:
- From a faulted ciphertext it computes 𝛼 and 𝛽
- Looks at IN[𝛼][𝛽] and deduce a list of candidates for x.
- From the x stored in the table XOR all the input bytes to recover the round key byte candidate k.
- Keep the list of the round key byte candidates.
- Then until the intersection of all the lists of candidates does not have a unique element repeat the previous steps.
On average, we would need only two faulted ciphertexts to recover one round key byte. Thus, we would need eight faulted ciphertexts to recover the full round key. As soon as the round key is recovered, we can invert the last round and apply the same attack on the previous round, and so on. As soon as we have recovered four round keys we can invert the key schedule and recover the secret key. On average, we would need a total of 32 different faults. The papers about SM4 fault attacks often have an experiments section to show the performances of their attacks but they never released the software to reproduce their results. However, we found an implementation of the previous fault attack, and we used it as a starting point.
This attack has the advantage to be practical since the faulted ciphertext only differed from the correct ciphertext by only five bytes. For example, we have simulated faults at the last round and if we XOR them with the correct ciphertext (the first value in the previous list) we have the following patterns:
It is really convenient to sort the fault in a huge list of random looking ciphertexts. We have implemented this attack in a tool called phoenixSM4 which is integrated in the great repository of the side channel marvels. This tool can be easily installed as a Python package:
pip install phoenixSM4Applying this attack on the previous faults would allow to recover the last round key byte per byte.
Then we tried to applied this attack on a more interesting case. We used a tool we developed called Glitchoz0r 3000 presented during R2Con 2020 to inject faults in a ARM binary using a C implementation of SM4. We emulate a fault skipping an instruction and we collected all the resulting faulted ciphertexts.
But then we sorted our fault to find the same pattern we were not able to find it. Nevertheless we had other interesting patterns:
But we could not apply the fault attack directly. We looked back at the academic literature and we figure out an extended fault attacks publish in 2007 by Li and Gu. The main idea of the attack is to inject the same fault but one round earlier. In this scenario, the fault would propagate to the full word at the next round and impacts all the bytes of the SBox inputs.
Since the inputs and the last round output are still available, we can apply the previous attack but this time in parallel on all the round key bytes. One word is still not impacted by the fault and it allows to still filter the faulted ciphertexts according to this pattern. In fact, the paper is going even further by analyzing faults happening even one round earlier, and in this case, only two faults allows to recover two full round keys in a row.
We implemented this attack as well and we found out that it is possible to combine this attack with the previous one by keeping the key byte candidate between each fault. It allows to exploit fault happening at the three last rounds. As soon as a round key is recovered, our tool will revert the round and continue the attack until four round keys are recovered. We also noticed that the extended attack does not apply to the second round since the output is not directly observable. For some fault happening in hardware, the computation of T was faulted directly but not the input register value. Consequently, for this kind of faults, the attack is still applicable and it extends the applicability of the fault attacks to this word as well.
Thus we tried our tool on the previous faults we collected before:

We can see that a round key is fully recovered for some steps and not byte per byte like previously. Then from the four round keys, it is possible to get back to the secret key with the inverse key schedule we implemented in Stark:
$ ./sm4_keyschedule C337204D D1C1C4AF 19237F5D AB6618FE 32
Key: 01234567 89ABCDEF 12345678 9ABCDEF0
K00: A292FFA1 DF01FEBF 7549C7EF 28CCFC2C
K04: F12186F9 41662B61 47E428DB 2CE3DB57
K08: 75E66F59 143D5E48 60FDA097 34E52BB1
K12: 8F014121 9DB355C8 5E7B4216 9AEFF625
K16: 6B384C62 1B0BD5D1 6C16B475 EA885F28
K20: 6B0F7ED5 60D23EC0 328B69B7 FA3386F7
K24: 7814E4E0 37128B07 BB1231C6 CCDA92E7
K28: 2480AF60 14024020 92E84954 85499C75
K32: C337204D D1C1C4AF 19237F5D AB6618FEThis fully recover the secret key.
We tested our tool on the faults generated on the real hardware. We used EM fault injection with NewAE’s ChipShouter using pulse of 400V and 150ns duration and the stock clockwise coil.
After a scan of several days we obtain some interesting faulted ciphertexts for a plaintext set to “A” sixteen times. We used our tool on them:

This demonstrates that the SM4 implementation of this SoC is vulnerable to low-cost fault injection. Our tool is published as open-source, and we encourage you to test it and even correct or improve it.









