I recently presented work on the analysis of a file encryption solution that claimed to implement “AES-1024 military grade encryption“. Spoiler alert: I did not break AES, and this work does not concern the security of AES. You may find advanced research regarding this topic.
This project started during a forensic analysis. One of my colleagues came with a USB stick containing a vault encrypted with SanDisk Secure Access software. He asked me if it was possible to bruteforce the password of the vault to recover the content. I did not know this software thus, I started to research. It appeared that this solution is distributed by Sandisk by default on any storage device you buy from them.
The solution is convenient, it allows a user to run the binary on the disk and after entering her correct password her vault is unlocked and the files are accessible. Once the software is closed, the files are encrypted back and not accessible anymore. So far nothing uncommon, but one thing drew my attention. In the Options menu, you can choose your “Preferred encryption method“.
I could choose ( if I would bought the premium version of the software) between several methods: “AES 128 bit“, “AES 256 bit“, “AES 512 bit” and “AES 1024 bit“. It was surprising to me since AES keys are defined in the standard to be either 128, 192 or 256-bit long but not 512 nor 1024 bits. Thus I was definitely interested to know what was behind this solution.
I dug a bit deeper and I discovered that the solution is developed for SanDisk by a company called ENCSecurity. The interesting part is that the solution is general and distributed to Sony and Lexar as well under different names. ENCSecurity also sells their own paying version with more options. I was surprised that the solution was not supported yet by John the ripper nor Hascat. In addition, the security claims of their website are really strong.

They claimed to provide “Ultimate encryption using 1024 bit AES keys, Military grade”. Thus for all those reasons, I decided to analyze the solution to figure out how it was implemented.
The binary is a PE packed with UPX. PE explorer allowed me to unpack it and still run properly. In the ENCSecurity version of the software, an option allows enabling the log of the application. At the beginning of the log I had:
05:11:42.633 D utils.cpp 372 showMessage returned 0
05:11:42.633 I encmainwindow.cpp 738 Starting ENCDataVault70 version: 7.1.1W
05:11:42.633 I encmainwindow.cpp 739 Date: 28.04.2021 05:11
05:11:42.633 I encmainwindow.cpp 740 Qt library version: 5.9.6
05:11:42.638 I encmainwindow.cpp 741 OpenSSL system library: OpenSSL 1.0.2q 20 Nov 2018
05:11:42.638 I encmainwindow.cpp 742 OpenSSL version: OpenSSL 1.0.2q-fips 20 Nov 2018
05:11:42.638 I enclogging.cpp 322 Application name: "ENCDataVault70"
I knew it used OpenSSL and Qt libraries and I got the version number as well. It allowed me to create a Ghidra Function ID database on the same libraries and Ghidra matched some of the function signatures in binary. It simplified a lot the analysis since all the Qt functions could be left apart since they concern the GUI and the interesting functions use OpenSSL for Cryptography algorithms.
In fact from a general point of view, I was analyzing a password hash function. The function takes as input a user password and hashes it to a key which is later used to encrypt or decrypt data. Usually, the password hash function takes as input a unique and randomly generated salt to avoid precomputed attacks like dictionary or rainbow table attacks. Another common parameter of the hash function is the iterations number which allows to adapt the work factor. The higher the iteration number is the longer it will takes to compute the hash and thus, the harder it will to bruteforce the password for an attacker. Currently the are various recommended algorithms like: PBKDF2, Scrypt or Argon2. Argon2 is the winner of the Password Hashing Competition and is now considered as the state of the art for password hashing.
For this analysis, I only needed to focus on PBKDF2. Its design is simple:

It uses a HMAC function with the user password used as the input key. The input message is simply the salt concatenated with the constant 1. In the previous figure, c is the number of iterations. At the end we obtain a key. However with the current construction, the key cannot be larger that the output of the HMAC. So how do we construct 1024-bit keys? PBKDF1 was originally designed with this limitation. However, in PBKDF2, the solution was found to iterate several time the construction but with the input message to be the salt concatenated with constant 1 to obtain the first key part key[1], then the constant 2 is used to obtain the second key part key[2] and so on … Then the derived key is simply the concatenation of all the key part obtained during the iterations.
If we go back to our binary, the key derivation function was not identified directly by Ghidra Function ID and I had to reverse it manually. Thankfully, some calls to the MD5 hash function were identified under several layers of calls. Finally, after some efforts, I was able to reverse it. Here is how it looks:

The design is similar to PBKDF2 but they used MD5 hash which is not an HMAC function. The last thing missing was the generation of the salt. I struggled hard to find where this was generated but finally, I figured out it was hardcoded in the code directly.
It looks randomly generated but it is definitively not unique since all vaults created with the software would use the same salt for the key derivation. In addition, users using the same password would end up with the same decryption key. Later I discovered that the same salt value is also shared among all the vendors: SanDisk, Sony and Lexar. A less critical problem is that the number of iterations is also fixed and set to 1000. This number of iterations was good when PBKDF2 was designed but nowadays the iteration number has to be higher. For example, OWASP recommends now 310000 iterations when PBKDF2 uses HMAC-SHA-256. Nevertheless, the construction itself of the key derivation function is flawed.
The part in red does not depend on the salt or the constant. Thus it allows making precomputation attacks even if the salt is randomly generated by precomputing the part in red and XOR the result with the salt afterward. It also reduces the complexity of generating large keys since the part in red can be reused at each iteration. This shows once again that trying to implement custom Cryptography often leads to failure. This was the first problem I reported to ENCSecurity and CVE-2021-36750 was issued for this problem. ENCSecurity later patched the problem by using OpenSSL implementation of PBKDF2-SHA256 together with a randomly generated salt and 100000 iterations.
Now that I got the key derivation function, I checked how the password was verified to be correct. In fact, a file name filesystem.dat sored in the folder C:\Users\user\AppData\Local\ENCSecurityBV\ENCDataVault70\ENCDataVault contains an encrypted magic value. When the decryption of this magic value gives 0xd2c3b4a1 then the password is considered correct. The decryption algorithm used OpenSSL AES encryption. In fact for the AES-128 option, the encryption is simply AES in CTR mode with a 128-bit key generated from the key derivation function described earlier. However for the other modes the construction is more curious.
It uses multiple AES encryptions. Two for AES-256 option, four for AES-512 and eight for AES-1024. Each time AES encryption is performed with a 128-bit key. The key parts generated previously with the key derivation function are XORed to the first eight bytes of the nonce prior to the encryption and finally, all the results are XORed together. Once the password is checked to be correct eight file encryption keys are decrypted with the same algorithms. Those keys are used to encrypt and decrypt the file stored in the vaults. This is a common way to proceed since it prevents re-encrypting all the files if a user changes her password. Only the file encryption key has to be re-encrypted in this case.
I got everything I needed to implement a John the ripper plugin that allows everybody to bruteforce AES-1024 military grade encryption! The plugin is now integrated into the main repository and also includes also the bruteforce of the new key derivation function based on HMAC-PBKDF-SHA256.
The latest point I needed to elucidate was how the files themselves are encrypted. First I thought they used the same encryption algorithm based on AES. For AES-128 is still the same method, AES in CTR mode. However, I was not able to decrypt the vault using other options. I came back to Ghidra and reversed the algorithm further. It turned out that the file decryption algorithm is different.
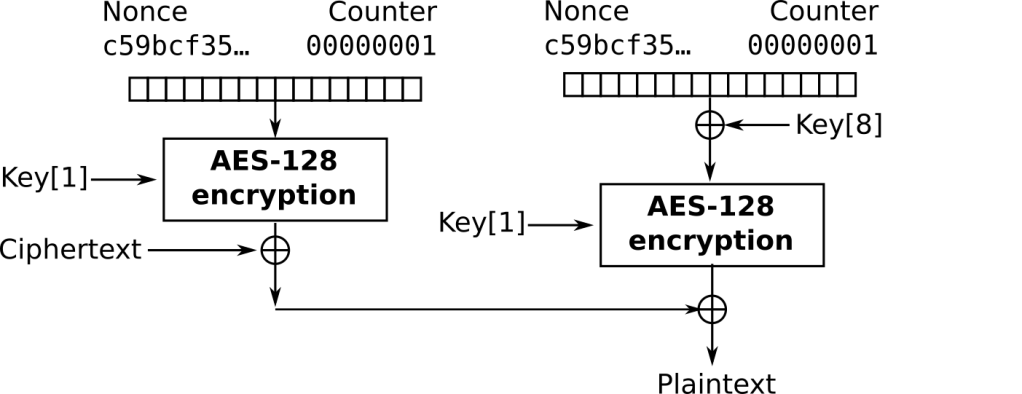
It appears that only two iterations of AES is performed for any other option and only the last file key, for example, key[8] for AES-1024, is used and XORed with the nonce and counter. However, the construction is closed to CTR mode of operation and thus also has the malleability property. It means that if an attacker has access to the encrypted data he can make modifications that would not be detected during the decryption and the same modification is applied to the decrypted file.
In addition, the previous construction gives only a maximum security level of 256 bits since we theoretically have to bruteforce the first file key, key[1], and the last one key[8]. But we can do more, if we assume we know that two blocks that have the corresponding plaintext equal to zero we can write the following formula.
The plaintext is not involved in the equations since it is zero. Then we can decrypt each part of the equations to have:
Finally, we XOR both equations and we obtained the following result.
There is no further dependency on the last file encryption key and thus it shows a reduction to 128 bits of security. Indeed we only need to bruteforce the first file key until we obtain the right part of the equation which is known. We made the assumption that we had found two separate blocks matching the encryption of a zero block. In fact, files are encrypted in a way that includes some zero blocks. Let’s look at the encrypted file format.

The IVs are in clear followed by the file name length. Then the file name is stored encrypted followed by zero blocks until offset 0x200 where the encrypted file content starts. Thus, our previous analysis holds for this solution and shows that we have only a level of security of 128-bits for all the encryption options. Those problems were also reported to ENCSecurity and CVE-2021-36751 was attributed to that.
This analysis shows again that it is difficult to roll a custom cryptographic algorithm and also that the level of security of a solution does not depend on the number of encryptions performed.







Whoa, I remember that software. A hard coded salt seems really silly, and you’d expect such big companies to know better. Really makes me think twice about who we can trust for secure encryption solutions.
Good job