Power analysis basics

 0. PREFACE

Recently I gave a two-hour workshop about power attacks at PHDays conference. After the workshop, I understood that two hours are not enough to present and explain power attacks to people who never worked with Side Channel Analysis before. Luckily, I was invited to give a 4-hour workshop at ZeroNights, so I would like to make a series of posts to explain power analysis attacks in a better way and then use these posts (and, hopefully, comments) to improve my workshop at the forthcoming conference. I will try to make high-level yet detailed enough explanations, otherwise the workshop may require more time.

1. INTRODUCTION

Power attacks is a group of Side Channel Attacks that analyze devices’ power consumption to:

• extract binary data; for example, secret keys of cryptographic algorithms;
• understand timing of a particular operation;
• dump the opcode values (Side Channel Based Reverse Engineering.

This looks unrealistic but statistical methods applied in Side Channels can distinguish a bit switch 1 to 0 from a bit switch 0 to 1. Since these operations can be distinguished, an attacker can extract processed binary data and get confidential information.

This post explains the very basics of power attacks, namely, when digital circuit consumes power, how power consumption can be modeled and thus used to reveal algorithms’ data. At the end of the post I will explain how power traces measured during DES execution can be analyzed to get the correct 6 bits of a DES round key. Some of the Side Channel Attack properties were discussed in the previous post ‘Timing attacks – Part 1’, so I encourage you to read that post first.

2. DIGITAL DESIGN IN THE EYES OF POWER ANALYSIS

Typically digital hardware contains two types of elements:

• Logic, i.e. combinatorial elements such as ALUs, muxes, control, etc. that process data but can’t hold a state.
• Registers, i.e. elements that keep their state until an external event arrival, such as clock or reset.

Any operation from a simple exclusive-or a comprehensive digital design (including cryptographic algorithms) can be implemented in logic. Theoretically, an entire algorithm can be created just with logic cells without using any register. However, apart from the complexity, such design would require huge area and the circuit would be too slow. To keep logic simplicity and re-usability, intermediate values can be kept in registers. In this case, the design becomes sequential: registers are updated, logic processes new values, registers are updated again, etc. The synchronization of operations is done using the clock. The clock signal guarantees that all the subcircuits finish processing old data before processing the new one, so there is no ambiguousness in the system.

An arithmetic logic unit (ALU) is the most typical example of the logic-register symbiosis, where logic performs operations over general-purpose registers. In a case of a block cipher (another typical example) logic implements one round while registers keep keys and intermediate round states (as shown on Figure 2).

The workflow of a typical digital circuit, illustrated on Figure 1, can be described as follows:

1. A new value is written to the register on a clock rising edge.
2. Logic starts processing the new value immediately after a register’s update.
3. After awhile logic finishes processing new input, so the system enters into a stable mode. This mode is necessary because register value can be updated only if the input is stable.
4. The entire system waits for a new clock. On a clock’s arrival a register value is updated and the entire process starts all over again.

CMOS logic consumes most of the power during the transaction. A transaction is simply an operation when a cell (register or logic) changes its state. Transactions in logic occur when a new input value arrives, while a register waits for a clock signal. Since registers and logic are coupled together, logic does not perform any operation until a new value is written to a register (register is an input for logic cells). Once a register is updated, a new value starts propagating via logic as illustrated on Figure 1. After some time logic generates a final result and the entire system enters into a stable mode when no more transactions happen, thus, no power is consumed. Since a register is synchronized within the clock, most of the power is consumed after the clock’s rising edge when a register value is updated.

A register consumes power only if a current value is overwritten by another, namely switches 1-to-0 and 0-to-1 consume power, while 0-to-0 and 1-to-1 don’t. This difference links the number of switched bits with consumed power; therefore, processed data can leak through power consumption making Side-Channel Attacks feasible.

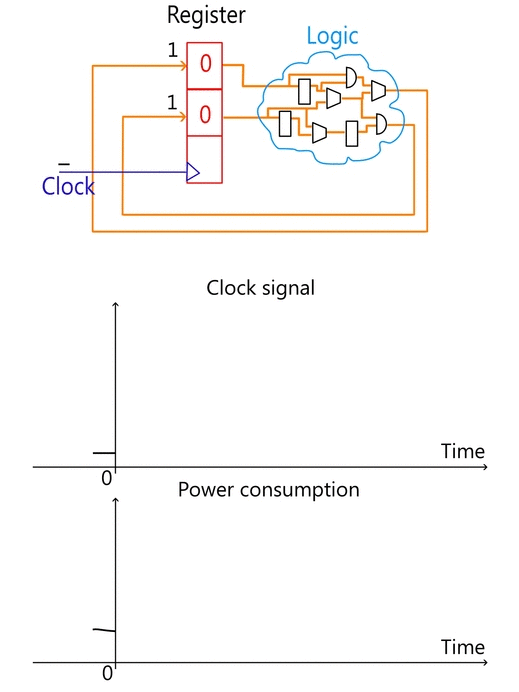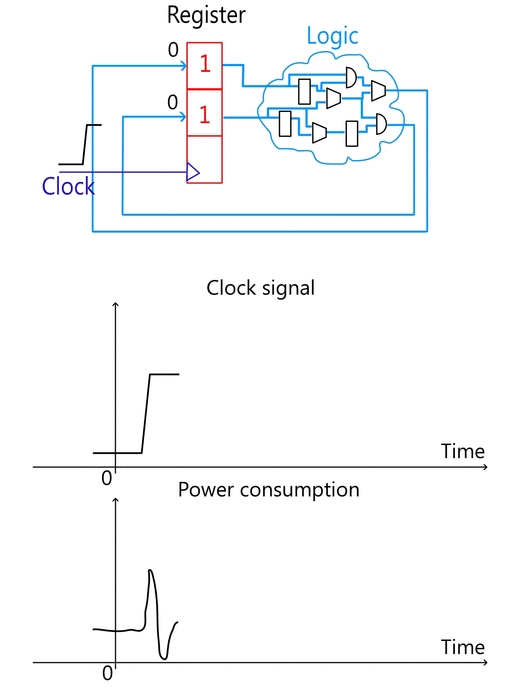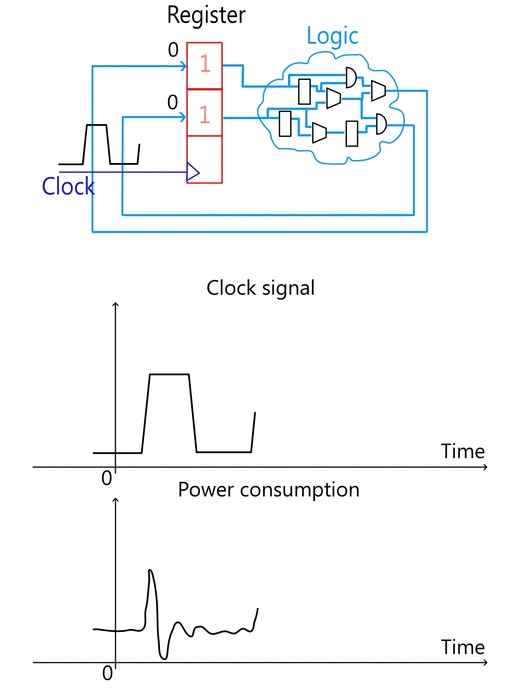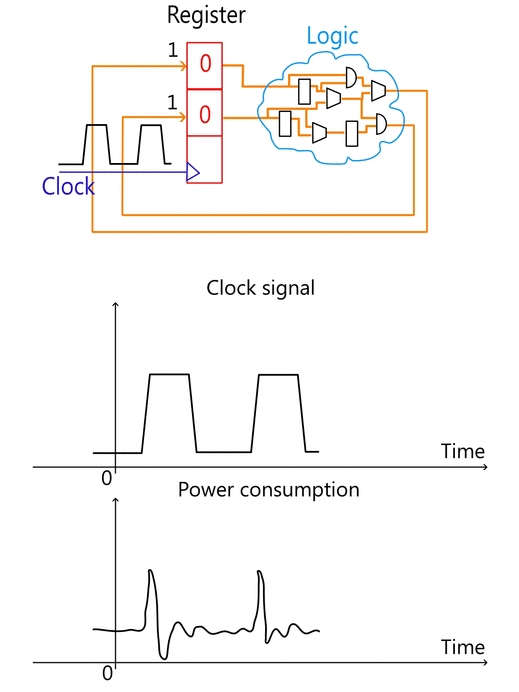
 Figure 1. Typical workflow of a digital circuit (clickable).

 

For the moment I want to emphasize that power consumption in a CMOS circuit has the following properties:

1. Most of the power is consumed on clock rising edge.
2. Power consumption depends on a number of transactions, i.e. the number of bits that were switched in a register.

Those properties are used to extract information about various algorithms including but not limited to: algorithm’s execution time, time of particular operations, processed binary data and other. Differential Power Analysis (DPA) is the simplest method that uses the above properties to extract secret key of cryptographic algorithms and the following part explains how this extraction can be done.

 3. DIFFERENTIAL POWER ANALYSIS

The first step of any power analysis is power acquisition. In this post I don’t explain the details of power measurement; however, I explain one important fact that all the traces are synchronized in time.

Consider an example of DES algorithm implemented in hardware. Each DES round is executed during one clock, i.e. 16 clocks needed to complete encryption. Both plaintext and ciphertext transfers are performed in series of 8 bits, so 8 clocks are needed to transfer plaintext and 8 clocks are needed to transfer ciphertext. DES implementation uses two 32-bit registers to keep L and R values, plus sixteen 48-bit registers to keep round keys (brief schematic of a DES hardware implementation is shown on Figure 2, this figure does not illustrate plaintext and ciphertext transfers).

Figure 2. Schematic of DES hardware design (clickable).

The power measurement is performed during plaintext transfer, encryption process and ciphertext transfer. Operations before plaintext and after ciphertext transfers are not measured.  The most typical way to start acquisition is to generate GPIO trigger when plaintext transfer is launched. Oscilloscope can recognize the trigger and start measuring power consumption.

Power trace of each algorithm execution (both transfers and encryption) has N points. Traces synchronization means that for any two traces a sample at time t is taken at the same digital circuit state (at the same algorithm step). The most important is synchronization of registers transactions and stable clock helps to achieve it. Fluctuations in acquisition/execution time are possible, bigger jitter would just increases the number of power traces required for successful key extraction.

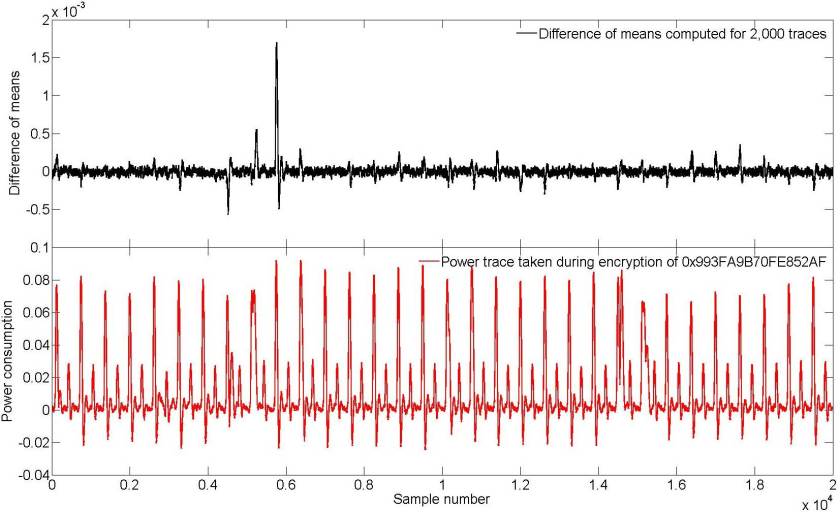
Figure 3 illustrates power traces acquired for two different DES executions (DES hardware was implemented as discussed above). Those traces were taken from DPA contest 1. As it can be seen both acquisitions are synchronized (at least the splashes, related to clock signal, are well aligned). 2,000 encryptions were performed and power consumption of each encryption has 20,000 points: approximately 5,000 first samples were taken during the plaintext transfer, 10,000 during all 16 rounds of DES, and the last 5,000 during the ciphertext transfer.

Figure 3. Power consumption for DES encryption (clickable).

The encryption process was measured from the beginning till the end; hence, we have the power information about different circuits’ states at each algorithm step. Power traces shall contain samples taken at the moment of register transactions, Sbox computations (if present) and etc.

As discussed, the above transactions 1-to-0 and 0-to-1 consume power, while 0-to-0 and 1-to-1 don’t. Let us consider a first bit of a register R. At the first round (first clock during encryption) this register contains plaintext after Initial Permutation operation, we denote this value as R1, at the second round (second clock during encryption) this register is rewritten with a new value which is an exclusive or between L register and an output of a Fiestel block, i.e. R2 = L1 ⊕ F(R1, K1):

R1 is overwritten by L1 ⊕ F(R1, K1)

Both R1 and R2 are stored in the same register, so at the moment of transaction a power shall be consumed according to the number of switch bits. Consider only the first bit of register R. When we know the plaintext and the key value we can split all the encryptions into two groups:

1. First group includes encryptions where the first bit of R was flipped during register update from R1 to R2.
2. Second group includes encryptions where the first bit of R was not flipped during register update from R1 to R2.

When we have N encryptions each group shall approximately have N/2 elements. If we find a difference between a mean value of traces from the first group and mean value of traces from the second group then we shall see a spike at the moment when the first bit of R is overwritten (see Figure 4).

Figure 4. Difference of means for 2,000 power traces computed for the correct key (clickable).

Why we see the spike at one place and other points are close to zero? The mathematical reasoning is explained in my previous post: “the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed”. If we don’t select traces and compute the mean value for all of them then the expected value during register switch would be T (the averaged number of flip flops in a register). Since the first group contained traces that have transactions at the first register’s bit the mean value would tend to T+A1, where A1 is an impact of one transaction. The second group contained traces without transactions, thus the mean value would be close to T-A2, where A2 is an impact of no transaction (A1 is not necessary equal to A2, however we may assume that A1=A2 without loss of generality). Thus, the difference between mean values at the moment of register switch would tend to A1+A2. Mean values for other samples would be close to the expected value, thus their difference would converge to 0. This fact is difficult to understand for the first time, however, after practicing this property becomes clear.

For that moment I’d like you to take the following into account:

1. The average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
2. When a prediction of bit transaction is done correctly, then the difference of means has a spike at transaction time.

However, how this can be used for an attack? Consider a situation when we use a wrong key. In this case prediction of bit transaction will be wrong and the first group would contain traces with and without transaction. The second group would also contain traces with and without bit transactions because bit prediction is done wrongly. Therefore the mean values of both groups will tend to T and the difference of means will not contain a spike. This fact is illustrated onFigure 5 when difference of means was computed for a wrong key value.

Figure 5. Difference of means for 2,000 power traces computed for the wrong key (clickable).

Therefore the spike appears when bit transaction is predicted with the correct key, while wrong key would result in ‘flat’ difference of means.

Note, that the prediction is done only on 1 bit transaction. In case of DES algorithm 1 bit of the first round can be predicted with 6 bits of the key, therefore the key value can be recovered by parts.

4. TO BE CONTINUED

Well, this was the first insight into power attacks. The method presented above is the simplest way to perform DPA. Advancements in power attacks will be covered step by step in my following posts.

DPAcontest site contains a repository with traces and code examples so a reader can try to perform power attacks against various algorithms.